This is part of a series of articles that solves popular puzzles and demonstrates the applicability of the puzzle-solving hobby to everyday life. If you love puzzles like I do, and you have a favorite that I haven’t written about yet, please send it to me! I haven’t seen a new one in a long time, and I’d appreciate your message.
Today’s post addresses three puzzles that are all similar to the recent “Three Slips of Paper” puzzle: Monty Hall, Bertrand’s Boxes, and The Three Prisoners. They are as follows:
Monty Hall
This puzzle is named for an old American television game show called Let’s Make a Deal, and more particularly for its host, Monty Hall. On that game show, contestants were sometimes presented with three doors, each with a prize behind it, and asked to pick a door (numbered 1, 2, or 3); the contestant would then receive whatever prize was behind the door. It might be something really nice, like a car, or it might be something less desirable, like a cheap coupon. The puzzle goes like this:
You’re a contestant on a game show. The host presents you with three doors to choose from, and informs you that behind the three doors are a goat, another goat, and a new car – but of course he doesn’t tell you which is behind which door. You are going to pick a door, but then before you see what’s behind that door, the host (who knows what’s behind all the doors) will open another of the doors to reveal a goat. You will then have the option to either take whatever prize is behind the door you initially chose, or you can switch to the other still-unopened door and take whatever prize is behind that door. How can you maximize your odds of getting the car?
It was popularized by Marilyn vos Savant.
Monty Hall Solution
First off, obviously when you pick a door the first time, your odds of picking the door with the car are one in three. The “trick” of this puzzle comes when the host then subsequently reveals one of the goats. A lot of people, upon first confronting this puzzle, think that the reveal increases the odds of finding the car to one-half; they figure that once the goat is revealed, each of the remaining doors has a one-in-two chance of hiding the car. That reasoning, however, ignores the contestant’s act of selecting a door. See, that first contestant-selected door had only a one-in-three chance of concealing the car, so when the host opens one of the other doors to reveal a goat, that collapses the remaining two-thirds probability that the car was not behind the contestant-selected door into the remaining unselected, unopened door. To prove it, here’s the decision tree:

Bertrand’s Boxes
Bertrand’s Boxes is named for Joseph Bertrand, who published it in his book Calcul des probabilités, published in 1889.
You are confronted with three boxes: one that contains two gold coins, a second that contains one gold coin and one silver coin; and a third that contains two silver coins. You select a box at random and draw a coin at random from that box. The coin happens to be gold. What are the odds that the remaining coin in the box is also gold?
Bertrand’s Boxes Solution
Having just seen the Monty Hall puzzle, you probably figured out pretty quickly that the answer is two-thirds. However, most people seeing this puzzle for the first time figure that drawing a gold coin narrows the puzzle down to two boxes, one of which contains two gold coins, and they’ll figure the odds are one in two. As with other similar puzzles, however, the answer is readily discernible using a decision tree:
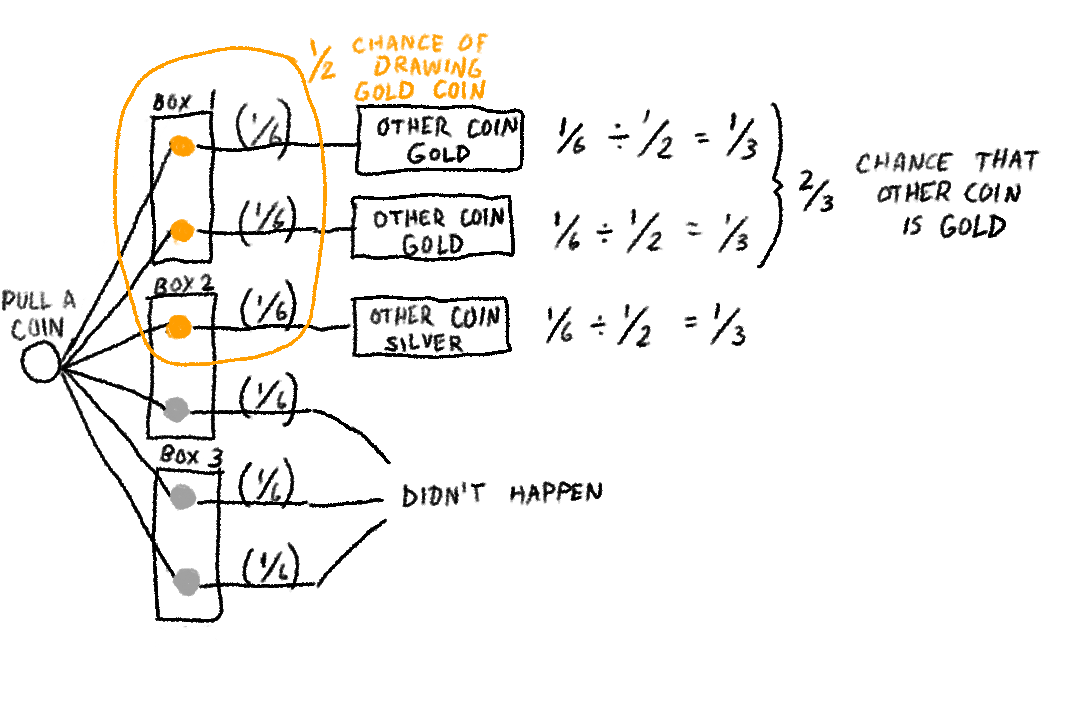
Just eliminate the possibilities that didn’t happen, then do the math on the remaining possibilities.
The Three Prisoners
The Three Prisoners puzzle was published in Martin Gardner’s Scientific American column in 1959. I grew up on Martin Gardner’s books of puzzles, and thoroughly loved them. Here’s his formulation:
“Three prisoners, A, B and C, are in separate cells and sentenced to death. The governor has selected one of them at random to be pardoned. The warden knows which one is pardoned, but is not allowed to tell. Prisoner A begs the warden to let him know the identity of one of the others who is going to be executed. ‘If B is to be pardoned, give me C’s name. If C is to be pardoned, give me B’s name. And if I’m to be pardoned, flip a coin to decide whether to name B or C.’
“The warden tells A that B is to be executed. Prisoner A is pleased because he believes that his probability of surviving has gone up from 1/3 to 1/2, as it is now between him and C. Prisoner A secretly tells C the news, who is also pleased, because he reasons that A still has a chance of 1/3 to be the pardoned one, but his chance has gone up to 2/3. What is the correct answer?”
I would add one more key piece of information: the warden agrees to Prisoner A’s proposal and does not lie.
The Three Prisoners Solution
Prisoner C is correct in his thinking; based on this new information, Prisoner C’s odds of being pardoned are two-thirds.

As in the Bertrand’s Boxes puzzle, just draw out the decision tree, then eliminate the possibilities that didn’t happen. In the puzzle scenario, the warden said that Prisoner B would be executed, so this eliminates the scenarios wherein he said that Prisoner C would be executed. That leaves two possibilities: one in which the warden says that Prisoner B will be executed and Prisoner A gets pardoned (one-in-six overall chance) and one in which the warden says that Prisoner B will be executed and Prisoner C gets pardoned (one-in-three overall chance). Because the warden’s statement eliminated all other possibilities, add up the odds and divide out to determine that, where the warden says B will be executed, C has a two-thirds chance of being pardoned.
Of course the odds would be different if the warden had, entirely of his own volition and without any structure, simply announced that Prisoner B would be executed. In that scenario, there would then be a 50% chance each for A or C to be pardoned. The critical element of the puzzle is that the warden agrees to follow the system set out by Prisoner A.
The Point
It’s good to look at these three similar puzzles together because it emphasizes the fact that the solution to a seemingly esoteric and obscure situation can be applied to other challenges in life. Even though the decision trees for these three puzzles are drawn differently, they are mathematically the same. The different decision trees represent different valid ways to approach the same basic puzzle. Once you have internalized the way of solving these puzzles, you can be on the lookout for other opportunities to gain valuable information in life by carefully applying reason to the facts available to you.
These are also interesting puzzles to look at together with the preceding “Three Slips of Paper” puzzle, even though they are not identical to that one, because the fundamental thought process is the same. Once you know how to solve these information-probability puzzles, they’re a breeze.
