This is part of a series of articles that solves popular puzzles and demonstrates the applicability of the puzzle-solving hobby to everyday life. If you love puzzles like I do, and you have a favorite that I haven’t written about yet, please send it to me! I haven’t seen a new one in a long time, and I’d appreciate your message.
The Puzzle
I have seen this puzzle in many different places, but this particular phrasing is taken (with minor edits for clarification) from the Car Talk radio show.
“Three different numbers are chosen at random, and each is written on one of three slips of paper. The slips are then placed face down on the table. The objective is to choose the slip upon which is written the largest number.
Here are the rules: You can turn over any slip of paper and look at the amount written on it. If for any reason you think this is the largest, you’re done; you keep it. Otherwise you discard it and turn over a second slip. Again, if you think this is the one with the biggest number, you keep that one and the game is over. If you don’t, you discard that one too, and you’re stuck with the third.”
At first glance, you might think the odds of getting the highest number are one in three. But I wouldn’t be bothering to write this down if it were that simple, would I?
Solving Discussion
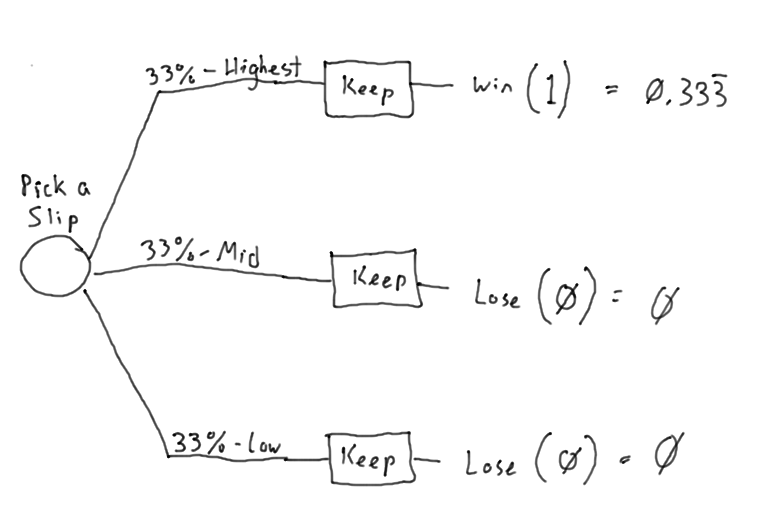
Any time you’re trying to maximize an outcome, your go-to tool should be a decision tree. They cover these things in business classes. It’s like a flow chart that reads left-to-right. Here’s what the decision tree looks like if you keep the first piece of paper you pull:
Assigning a value of “1” to a “win” where you found the highest number, and a value of “0” to a “loss” where you are stuck with one of the lower numbers, the expected value of this strategy is 0.333…. Which is just a fancy way of saying you have a one in three chance of getting the highest number this way.
Now, this becomes a pretty simple puzzle because there are really only three other strategies possible within the framework of the rules:
- Discard the first number you pull and keep the second.
- Discard the first and second numbers you pull and keep the third.
- Discard the first number you pull, look at the second number, and then decide whether to discard the second number and pull the third.
You can reason out pretty readily that options 1 and 2 are not different from just keeping the first piece of paper you pull. Option 3, however, is interesting because there’s a choice involved. Does that choice make a difference? If you want to work it out yourself, go ahead; this page will still be here. If not, read on…
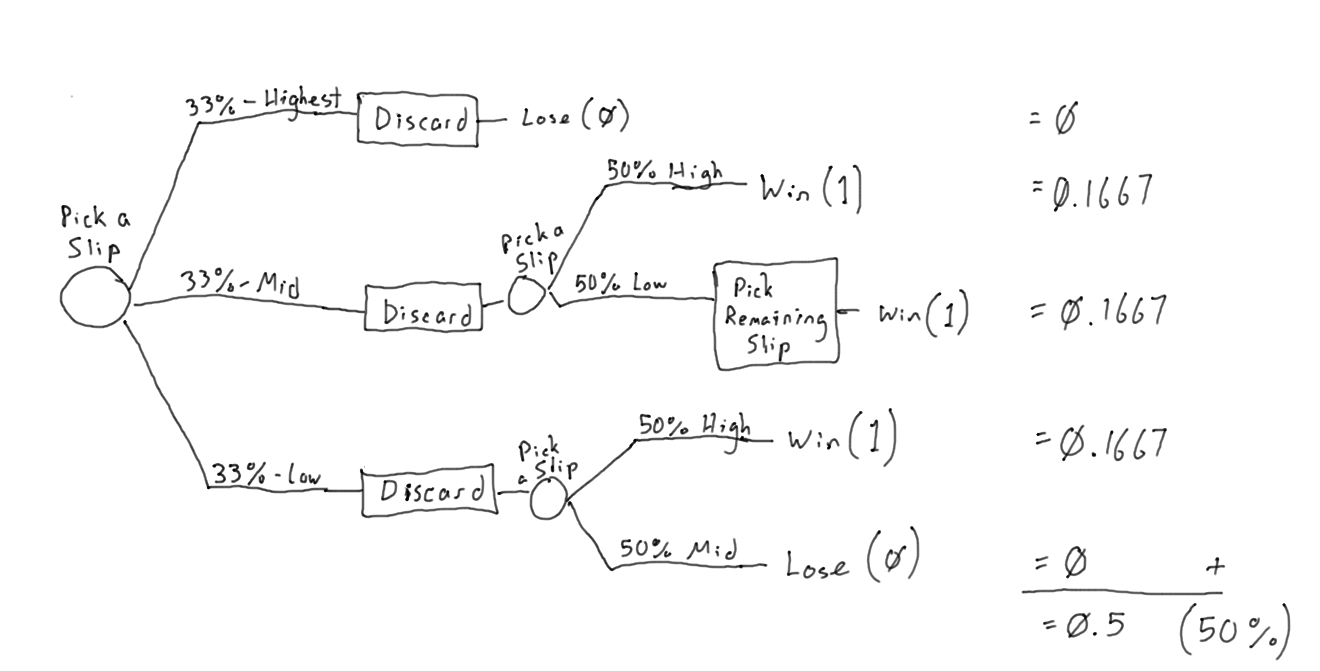
The winning strategy for solving this puzzle is to pull a number at random, look at it, discard it, and pull a second number. Then, if the second number is higher than the first, keep it. If the second number is lower, discard it and keep the third and final number. Here’s the decision tree:
So if you discard the first number you pull, there is a one-in-three chance that it was the biggest number and you lose. There is also a one-in-three chance that it was the middle number. If it was the middle number, and the second number you pull is the highest number, then by following the strategy you will keep it and you will win. If the second number you pull in this situation is the lowest number, then by following the strategy you will discard it and pull the third number, which will be the highest number, and you will win. So this strategy means you always win if the first number you pull is the middle number. This means that so far, we have a one-in-three chance of losing and a one-in-three chance of winning. What happens in the remaining one-in-three scenario where the first number pulled is the lowest number? Well, this means that the second number pulled will definitely be higher than the first, so we will keep it, and there is a one-in-two chance that it was the highest number and a one-in-two chance that it was the middle number. So on the one-in-three chance that the first number pulled is the lowest number, we have a 50% chance of winning and a 50% chance of losing. Adding all these percentages up, we have a one-in-three chance of losing, a one-in-three chance of winning, another one-in-six (33.33% times 50%) chance of losing, and another one-in-six chance of winning. That comes out to a one-half chance of winning and a one-half chance of losing. That’s better than the one-in-three chance given by random selection, so this is a superior strategy.
Beyond the Puzzle
It’s useful to work out this sort of small-scale puzzle to learn basic mathematical patterns, but in order to really wring every bit of value out of a puzzle and internalize the underlying concepts, it’s important to expand it and see how it can apply in other contexts. In order to solve the puzzle, we worked out what happens with a set of three numbers, but what happens with a set of ten? Should we just examine and discard the first selection? Examine and discard one-third of the numbers? Discard all but three of the numbers and then follow the strategy from the first puzzle? Follow some other strategy? Let’s find out…
First off, the odds are pretty easy to calculate if we decide to discard seven of the ten and then follow the strategy from the first puzzle. There is a 30% chance that the highest number remains undiscovered after discarding 70% of the numbers, and the first puzzle solution gives us a 50% chance of finding the highest of the three remaining numbers, so our overall odds of winning are 15%. This is a good check; it proves that the first puzzle still has value here. The odds of 15% beat the odds of 10% that we get if we choose at random. But can we beat 15%? Obviously, we can: if we just slightly modify the original strategy to say that we will discard the ninth number not only if it is smaller than the eighth, but if it is smaller than any of the first eight numbers, this of course slightly betters the odds. These first couple of intuitive tests having borne fruit, we are motivated to proceed to look for the best solution by working through the decision trees.
Let’s next look at the other obvious permutation of the strategy from the original puzzle: pick a number, look at it, discard it, then proceed to draw additional numbers until we find one that is higher than the first number. This gives us:
- a 10% chance of drawing the highest number first, in which case we lose;
- a 10% chance of drawing the second-highest number first, in which case the next number we draw that is higher than any preceding number will necessarily be the highest number in the set, which means we will win;
- a 10% chance of drawing the third-highest number first, in which case there is a 50-50 chance that the next number we draw that is higher than any preceding number will be the highest number;
- a 10% chance of drawing the fourth-highest number first, in which case there is a one-in-three chance that the next number we draw that is higher than any preceding number will be the highest number;
… and so on. You see the pattern. The odds of selecting the highest number via this method are (.1 × 0) + (.1 × 1) + (.1 × .5) + (.1 × .333) + (.1 × .25) + (.1 × .2) + (.1 × .1667) + (.1 × .1429) + (.1 × .125) + (.1 × .111), totaling about 28.3%. Already this is way better than any prior answer. But can we improve on it further?
Now let’s try drawing three numbers, discarding them all, and proceeding from there. The first thing you’ll notice is that your decision tree becomes a LOT more complex if you try to map out all the possibilities of which three numbers you might draw. In fact, there are 720 (ten times nine times eight) possibilities for what those first three numbers could be. We need to collapse this down some. So let’s think: which of these possibilities are alike? It turns out that the only thing that matters about those first three numbers is the highest number. Think about it: if the highest of the first three numbers is, let’s say, the second-highest number in the set, it doesn’t matter what the other two are. The rest of the puzzle proceeds the same. So, collapsing things down: in 216 out of the 720 possibilities, the highest of the three numbers is the highest number in the set; in 168 of the 720 possibilities, the highest of the three numbers is the second-highest number in the set; in 126 of the 720, the highest of the three is the third-highest in the set; in 90 of the 720, the highest of the three is the fourth-highest in the set; 60 of 720, fifth-highest; 36 of 720, sixth-highest; 18 of 720, seventh-highest; 6 of 720, eighth-highest; and of course if you have three different numbers out of a set of ten, the highest of the three can be no smaller than the third-smallest, which is also the eighth-highest. Add ‘em up and you get 720.
So what are the odds of victory in each of these scenarios? Well, if the highest number got drawn as one of the first three, we lose. And the rest of the odds track what we just worked out in the preceding scenario: 100% if the highest among the three is the second-highest of the set; 50% if the highest among the three is the third-highest of the set; one-in-three if the highest among the three is the fourth-highest of the set; and so on. Multiplying it out, our total comes to almost a 40% chance of finding the highest card! (39.75% to be precise). So by reviewing and discarding almost a third of the numbers, thereby accepting an automatic 30% chance of failure, we actually boost our overall odds of success!
Now, just for the sake of confirmation, let’s run the math if you discard four. … Actually, let’s not do that part together. If you want to, I hope you will, but I’m just going to give you the answer: 39.83%. And then if you run the numbers on discarding five, you get 37.28%. So we’ve identified a peak at around three or four cards discarded. The key seems to be to discard a third of the numbers. For example, if you have 12 numbers, the peak odds are 39.6% if you discard four cards.
The Point
Can you think of a parallel scenario from real life? A situation where you have to get “involved,” let’s say, with an unknown in order to learn its value, and then before you can learn the value of another unknown, you have to discard the first one? How about dating? After you’ve narrowed the field to a set of likely possibilities, you have to date one of your prospects in order to find out how compatible you are. But before you can investigate another prospect, you are typically going to have to discard the first one… and by the time you’ve investigated your second prospect, the first will probably be involved with someone else and therefore no longer an option.
The metaphor isn’t perfect, but it’s pretty good. As a young, single person looking for a relationship, you typically have no idea what the range of possible values are for relationship bliss. Even after you’re in a relationship, it’s impossible to tell how your relationship stacks up in terms of objective quality. You need to experience a few relationships in order to have some confidence that you’ve found a good match.
So to give a real-world example: let’s say you’re in college. Out of your fellow students, numbering 20,000, you winnow them down based on criteria such as age, religion, sex, socio-economic background, geography, similar interests, physical attractiveness, and maybe other factors to ten viable dating prospects. You could pick the one that, based on your best guess, seems best to you, but let’s face it: you’re not that far along in your life. There’s a pretty sizeable margin of error on your guess. Your best move is really to get some experience by dating a few people, and then start looking in earnest. If you have ten prospects, this puzzle suggests that your optimum strategy would be to try out four of them to maximize the value of your experiences. Of course this puzzle is just one equation among many that would inform an actual decision, but it does suggest a base experience level is necessary to learn enough about yourself and relationships generally to make further decisions with some degree of confidence. It also suggests that, if a person has a high number of potential mates, it makes sense to test out more of them before beginning to look in earnest.
The most obvious way in which this puzzle differs from reality is that it is not actually a loss scenario if you fail to end up with the best possible mate, and of course this fact changes the decision tree significantly. However, it does perhaps describe that persistent part of the human psyche that does feel like anything short of the “best” is failure.
This is a wonderful puzzle because it provides an example of how to think through decisions in a limited-information environment. Sometimes people lock up when presented with a decision and incomplete information, and will sometimes throw up their hands and make a decision at random; especially in a situation like this, where losing is more likely than winning. However, you can frequently increase your odds in an apparently hopeless situation by just carefully thinking through what you can deduce from the information you do have, and what else you can learn efficiently in the time you have.