This article looks at the refrigeration system patented by Albert Einstein and Leo Szilard and explores the underlying scientific principles.
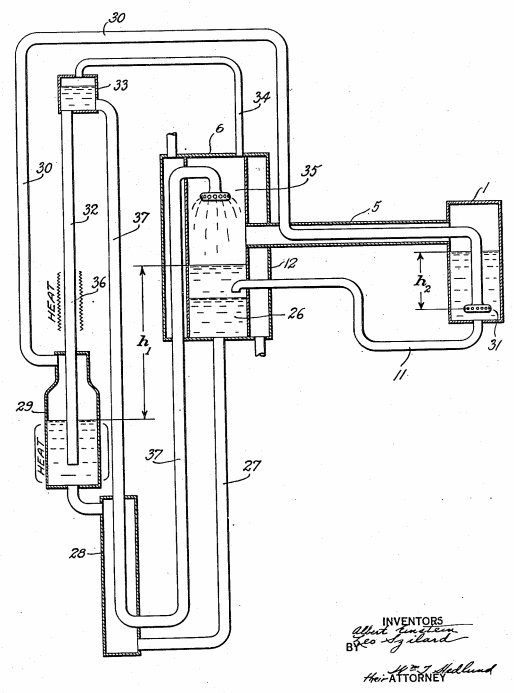
The refrigerator is depicted in the patent filed by Einstein and Szilard, a copy of which is available here: http://opensourceecology.org/w/images/6/63/Einstein_Fridge.pdf. It’s copied below, but you’ll want to go ahead and click that link so you’ll have the image as a reference.
As a quick orientation, the little box on the right, labeled “1,” is the part that gets cold. All the other things in the drawing are the parts that are necessary to make that little box get cold. Also note: if you wanted to use this system to, say, keep your food cold, you wouldn’t put the food in that little “1” box. No, the “1” box would go inside of a larger insulated box, and your food would go in there. The “1” box would get cold, heat would conduct from the inside of your insulated box through the walls of box “1” into its interior, and that in turn would make your food cold.
The fundamental principle by which this device makes cold is this: when liquids turn into gasses, they suck up heat from their surroundings. A mass of water vapor at 212 degrees Fahrenheit has more heat energy than the same mass of liquid water at 212 degrees Fahrenheit. One term for this concept is “enthalphy of vaporization.” It’s an interesting and powerful scientific principle. Just for example: it takes 5.4 times as much heat energy to convert water at a given temperature to water vapor at the same temperature as it does to heat the same water from 32°F to 212°F. This is why sweat is so effective at cooling you off: every ounce of sweat that evaporates draws in enough heat energy to cool three quarts of water by 10°F. [Can’t help adding: the specific heat of flesh is around 3,470 J/kg*K, so if you weigh 200 pounds, every 2.7 ounces of evaporated sweat is enough to cool your body 1°F.]
The Einstein-Szilard refrigerator, instead of using water as the evaporating substance, uses butane. Here’s how butane stacks up against water in some key properties:
| Water | Butane | |
| ΔHvaporization (kJ/mol) | 40.66 | 21 |
| ΔHvaporization (kJ/kg) | 2257 | 320 |
| Boiling Point | 100֗֠ºC | -1ºC |
| Density (liquid) | 1,000 kg/m3 | 600 kg/m3 |
| Condensation pressure at 100ºF | ~38 psi / 2.6 atm | ~1 psi / 0.068 atm |
| chemical formula | H2O | C4H10 |
So butane has lower enthalpy of vaporization than water, meaning you need to evaporate more of it to produce temperature change. How much more? Seven times as much by weight, and almost 12 times as much by volume. However, it has a couple of other key properties that make it more useful than water for this purpose. Mainly, its boiling point is much lower than water’s. Back to box “1;” the liquid butane is evaporated by the addition of gaseous ammonia, which is bubbled through the liquid butane by the porous stone “31.” The gaseous ammonia causes the butane to evaporate much like water will evaporate into air – even well below its boiling point – until it reaches 100% relative humidity. As the butane evaporates, it pulls in from its environment the energy required to overcome its enthalpy of vaporization, which makes its environment colder. Butane’s low boiling point and condensation pressure make it well suited for refrigeration temperatures.
As we’ve now established, all we need is a steady supply of liquid butane and a steady supply of gaseous ammonia, and we’ll have a steady supply of cold. The purpose of all of the other components of the Einstein-Szilard refrigerator apart from box “1” is to recycle the butane and ammonia so that you don’t have to keep supplying your cooler with fresh butane and ammonia. That would get expensive. Einstein and Szilard figured out a series of chemical processes by which the butane and ammonia could be recycled, requiring only a heat source and an environmental heat sink (such as the atmosphere, a lake, or a well).
Separating the Butane Vapor from the Ammonia Vapor
After the ammonia gas evaporates the butane in box “1,” the ammonia and butane gasses are combined. The first step in recycling them is to separate them. This is done by exploiting the fact that ammonia dissolves readily in water, whereas butane does not. This happens in box “6” on the diagram. The ammonia-butane gas mixture flows to box “6” via pipe “5.” [Note that pipe “30” passes through pipe “5;” we’ll get to that later.] In box “6,” water is sprayed through the ammonia-butane gas mixture using sprayer head “35.” The ammonia dissolves into the water and the ammonia-water solution falls to the bottom of the tank (“26″ on the drawing) because liquids are heavier than gasses. Removing the ammonia from the butane has the helpful side effect of condensing the butane (re-liquefying it), so the butane also falls to the bottom of the box, but it’s less dense than water so it floats above the water. This actually completes the recycling of the butane, and the butane is allowed to flow back into box “1” via pipe “11.”
Of course the butane warms back up as it condenses, releasing as much heat energy as it absorbed when it evaporated. This heat has to be dissipated before the butane goes back into box “1,” and that’s what the heat exchanger “12” is for.
Recycling the Ammonia
After the process in box “6,” the butane has been recycled, but the ammonia is now in solution with water. It must be returned to its gaseous state in order to be useful. To achieve this, the Einstein-Szilard refrigerator exploits another property of ammonia: more ammonia can dissolve in cool water than in hot water. In other words, heating the water-ammonia solution will force out the ammonia, which will return to its gaseous state. This heating is done in box “29.” The heat supplied to box “29” is the primary energy required to make this heat pump work.
The hot ammonia gas travels through pipe “30” to box “1.” On the way, it passes through pipe “5,” where it exchanges heat with the chilled ammonia-butane mixture that is exiting box “1,” so it enters box “1” pre-chilled and does not introduce too much heat to box “1.”
Recycling the Water
The byproduct of the ammonia recovery is hot water, which must be cooled so that it can again be useful for absorbing ammonia. In the original Einstein-Szilard design, this is done using the heat exchangers at 28 and 12. Heat exchanger 28 uses this hot, low-ammonia water to pre-heat the high-ammonia water en route from box 6 to box 29 while simultaneously cooling the hot water. Heat exchanger 12 requires an external heat sink such as a source of cool water – maybe water pumped to a geothermal heat sink. Air cooling could work, too, with some coils, a pump to move the cooling water through the coils, and a fan to move air over the coils.
This water cooling step is where a couple of common myths often claimed about the Einstein-Szilard refrigerator break down:
Myth #1: It’s a device that turns a heat source into a cold source!
Not entirely true. It’s impossible to make a system colder by adding heat. What the Einstein-Szilard refrigerator actually achieves is a heat pump, which is a device that moves heat energy from one place to another. Specifically, this one moves heat from the surroundings of box “1” into box “1,” then from box “1” to box “6,” then from box “6” into the environment via heat exchanger “12.” It is very interesting and useful that it does this without needing a motor, just a heat source, but of course it does not defy the laws of conservation of energy.
Myth #2: It’s a refrigerator with no moving parts!
Not quite. It’s true that it’s a heat pump with no moving (solid) parts, but heat pumps just move heat from point “A” to point “B” (or in this case from box “1” to heat exchanger “12”). Unless you have some mechanism in place to dissipate the heat from point “B,” the heat pump will overheat the environment at point “B” and stop working. In order to have what we think of as a household refrigerator, we need a fan or pump or some other way to keep the environment around heat exchanger “12” from getting hot.
Likewise on the cold side, some air circulation around box “1” would be needed so that it doesn’t get too cold right next to box “1” and not cold enough in the rest of your insulated box.
Once the hot water is cooled down, the cycle is complete and we are back to our starting products: gaseous ammonia, liquid butane, and unheated water. The Einstein-Szilard refrigerator continuously runs this process, cooling the surroundings of box “1” and heating the heat sink around heat exchanger “12.”
I intend to come back later and take a longer look at this style of heat pump, performing a somewhat more in-depth analysis. For now, I have enjoyed considering the key concepts that make the machine work. It will be a useful thing to consider for using waste heat from industrial processes to cool other processes. I hope I get a chance to use this concept.